
A magic square is a type of square that is populated with integers in such a way that the sum of the numbers of each row, column and both diagonals equal the same amount. In the example below, you can see a 5 x 5 unit square with the sum of the numbers in each row, column and full diagonal equaling 65.
65
|
17
|
24
|
1
|
8
|
15
| |
65
|
23
|
5
|
7
|
14
|
16
| |
65
|
4
|
6
|
13
|
20
|
22
| |
65
|
10
|
12
|
19
|
21
|
3
| |
65
|
11
|
18
|
25
|
2
|
9
| |
65
|
65
|
65
|
65
|
65
|
65
|
65
|

Magic squares have been around for over 4,000 years. They have been found in Egypt, India, and China, and were used as good luck charms because of the belief that they offered their wearers longer lives and health.
How to build it I am not sure how much healthier you will get if you wear one of these squares, but they are fun to build. To start you can either download my spreadsheet or follow these step by step instructions.
Start by drawing a square that is made up of an uneven number of rows and columns (i.e. 3, 5, 7, etc). You don’t have to start counting at number 1, but until you get the hang of it, I recommend you do.
Place your starting number in the top row and middle column (see Illustration-1). The main rule for placing all other numbers is to try and move diagonally upwards to the right. This rule has several exceptions that I will cover next.
Step-1 Move UP and to the RIGHT (diagonally) from the first number. If you can find an empty square (in Illustration-1 this would put you outside the grid), drop down to the bottom row of the column and place it there.

Illustration-1
Step-2 If you can, place the next number diagonally to the right of the previous number (Illustration-2).

Illustration-2
Step-3If you can’t place the number diagonally to the right and can’t drop to the bottom row of the column (in illustration-3 this would put you outside the grid), loop around (heading left and one row above from where you placed your last number).

Illustration-3
Step-4 If you can’t place the number diagonally to the right or place the number on the bottom row of the column (in Illustration-4 it’s taken by the 2), place the number directly under where you placed the last number (below 5).

Illustration-4
Step-5 Repeat steps 1 -4 until you’re finished.
You may find that completing the first square is a bit confusing, but don’t give up. After you go through a few practice runs, you will master the technique.
If you completed your magic square but are not sure if you solved it correctly, here is a formula for getting the sum for any odd sided magic square.
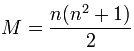
Where:
n = Square size (i.e. 3, 5, 7, 11, etc.).
M=Magic constant (the sum of the rows, columns, and diagonals)
For the magic square above this would be:
M = 5(5^2+1)2
M= 5(25+1)/2
M= 5(26)/2
M= 130/2
M=65
If after all this number crunching you still feel the need to experiment, why not create some magic square art. I call it “The Magic Flower”. It is made out of 6 magic squares sized at 3, 5, 7, 9, 11, and 13.


...you are just brilliant. Simply mathologically (is that a word?) surpassing others...it's mathical! Uh--I mean 'magical'!
ReplyDeleteThank you, Dawn… that is such an honor coming from a fantasmagorical…um I mean fantastic person like you!
ReplyDeleteLiebes Fraeulein Sieben, I tried this out - it works! I will get them busy with magical squares on Shabatt!!! YEEEESSSSS!!!
ReplyDeleteI thought of something smart to say to - but but but - Shachar said it all!!! She stole all the complimenting words from me!!! I I I wanted to say all that! Lucky for her she is a Lady, and even more lucky for her that I love her, otherwise I would have gone back at her!!! Yes, I would have thought of something, like stealing one of her stories!!!
Uff! :-)
Danke shoen, Yael. How did your magic squares work out?? I remember you told me that Uri studied math, can he share any interesting math tricks?
ReplyDelete